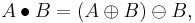Closing (morphology)
In mathematical morphology, the closing of a set (binary image) A by a structuring element B is the erosion of the dilation of that set,
where  and
and  denote the dilation and erosion, respectively.
denote the dilation and erosion, respectively.
In image processing, closing is, together with opening, the basic workhorse of morphological noise removal. Opening removes small objects, while closing removes small holes.
Contents |
Properties
- It is idempotent, that is,
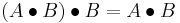 .
. - It is increasing, that is, if
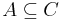 , then
, then 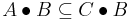 .
. - It is extensive, i.e.,
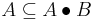 .
. - It is translation invariant.
See also
Bibliography
- Image Analysis and Mathematical Morphology by Jean Serra, ISBN 0126372403 (1982)
- Image Analysis and Mathematical Morphology, Volume 2: Theoretical Advances by Jean Serra, ISBN 0-12-637241-1 (1988)
- An Introduction to Morphological Image Processing by Edward R. Dougherty, ISBN 0-8194-0845-X (1992)